Concepto
Cómo se calcula la expansión térmica
La expansión térmica coeficiente volumétrico: 

Cambio en el volumen: 

Volumen final: 

Temperatura inicial: 

Temperatura final: 

Cuando, b = coeficiente de expansión térmica volumétrica, Vyo= Volumen inicial, VF= Volumen final, tyo= Temperatura inicial, tF= Temperatura final.
Aquí podemos encontrar una herramienta que hace el cálculo por ti (clic)
La expansión térmica lineal:
Coeficiente de dilatación térmica lineal: 

Duración inicial: 

Longitud final: 

Temperatura inicial: 

Temperatura final: 

Cuando, a = coeficiente de dilatación térmica lineal, Lyo= Longitud inicial, LF= Longitud final, tyo= Temperatura inicial, tF= Temperatura final,
Aquí podemos encontrar una herramienta que hace el cálculo por ti (clic)
Relación térmica lineal y volumétrico de expansión:
La expansión térmica coeficiente volumétrico: 

Coeficiente de dilatación térmica lineal: 

Cuando, b = coeficiente de expansión térmica volumétrica, a = coeficiente de dilatación térmica lineal.
Aquí podemos encontrar una herramienta que hace el cálculo por ti (clic)
Cálculo de tensiones teniendo en cuenta esfuerzos térmicos
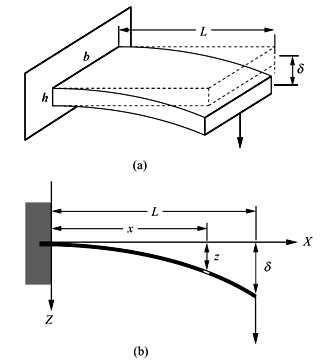
Si la barra de la Figura A, está fija en uno de sus extremos, por ejemplo empotrada, a causa de la dilatación térmica, se desarrollan esfuerzos en la misma, que se deben tener en cuenta para los cálculos del diseño de la pieza o de su instalación.
La deformación en la barra debido a las tensiones desarrolladas puede ser expresada como,
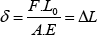
Donde F es la fuerza que actúa en la sección de la barra, Lo es la longitud original, A es el área de la sección y E es el módulo de elasticidad del material de la barra
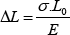
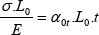
La deformación en la barra debido a las tensiones desarrolladas puede ser expresada como,
[3.9]
Donde F es la fuerza que actúa en la sección de la barra, Lo es la longitud original, A es el área de la sección y E es el módulo de elasticidad del material de la barra

Figura 3.5
Si a la relación F/A se expresa como σ (sigma) ;
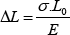
[3.10]
Si consideramos la dilatación debido a la temperatura,
ΔL = αot.Lo.t [3.11]
e igualando las expresiones [3.10] y [3.11], tendremos:
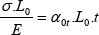
y finalmente
σ = αot. E.t [3.12]
Las tensiones desarrolladas a causa de una variación de temperatura, son directamente proporcionales al coeficiente de dilatación, al módulo de elasticidad y a la temperatura.
Valores de coeficiente de expansión térmica para distintos materiales
Ejemplo de viga biempotrada con una variación de temperatura resuelta en Abaqus




Comentarios
Publicar un comentario